BdMO Online Forum

$ABCD$ is a square. Circle with diameter $AB$ and circle with center $C$ and radius $CB$ meet inside the square at $P$. Prove that $DP = \sqrt2 AP$.

Here lets take $\angle DAP=\angle b$
So,$\angle PAB=90^o-b$.
We know hat $\angle APB=90^o$
Or, $\angle ABP=\angle b$
So, $\angle PBC=90^o-b$

Now, $\triangle CBP$ is isosceles such that $CP=CB$. We draw the angle bisector $CM$ of $\angle BCP$. Here $CM \perp PB$. And $\angle BCM=\angle b$.

Now by $ASA$ congruence, $\triangle PAB \cong \triangle CMB$. And also, $\triangle CMP \cong \triangle CMB$.

So, $BM=MP=AP$


Now, we had already showed that $\angle PBC=90^o-b$ .So, $\angle BPC =90^o-b$. So, $\angle BCP = 2b$.
So, $\angle PCD=90^o-2b$. Or, $\angle CPD= \angle CDP=45+b$.


And. $\angle APD=360^o-\angle APB+\angle BPC+\angle CPD$
Or, $\angle APD=360^o-\angle 90^o+\angle 90^o-b+45^o+b $
Or, $\angle APD = 135^o$. And so, $\angle PDA= 45-b$

Now, we had already showed that $PA=PM$. $\angle PAM= \angle PMA = 45^o$. And, $\angle AMP=135^o$

And, $\angle PAB =90^o-b$ and $\angle PAM= 45$. So, $\angle MAB= 45-b$, and we had showed far early that $\angle ABM=b$ [$B,M,P$ are lying on same line].

So, $\triangle DAP \cong \triangle ABM$.

So. $DP=AM$

We now had a right triangle $ \triangle PAM$

So. $cosec 45^o= \frac {AM}{AP} = \frac {DP}{AP}= \sqrt 2$
And finally, $DP=\sqrt 2 AP$

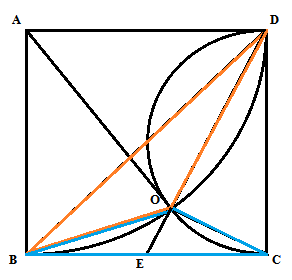
At first we connect A, O. Then B, D. Then connect D, O and extend it beyond O which will

intersect BC at point E.

$\Delta{}$ABO is an isosceles, where

AB = AO.

So, $\angle{}ABO\ =\ \angle{}AOB.$


Now, $\angle{}ABO\ =\ \frac{180^\circ{}\ -\
\angle{}BAO}{2}=90^\circ{}-\frac{\angle{}BAO}{2}$ .................(1)

Again, $\angle{}AOD\ =\frac{180^\circ{}\ -\
\angle{}OAD}{2}=\frac{180^\circ{}-\left(90^\circ{}-\angle{}BAO\right)}{2}=45^\circ{}+

\frac{\angle{}BAO}{2}$ ............... (2)

Now,
(1) + (2)

= $\angle{}$BOD

=$\ \ 90^\circ{}-\frac{\angle{}BAO}{2}$ + = 135$^\circ{}$

So, $\angle{}$BOE = 180$^\circ{}$ - $\angle{}$BOD = 45$^\circ{}$

Now, $\angle{}$BOC = $\angle{}$BOE +$\angle{}$EOC

= 45$^\circ{}$ + 90$^\circ{}$ [As, DE $\perp{}$ CO]

=135$^\circ{}$

Now, $\angle{}$BDC=45$^\circ{}$

Let, $\angle{}$BDO= b

So, $\angle{}$ODC=45$^\circ{}$ - b

So, $\angle{}$DEC= 90$^\circ{}$ - (45$^\circ{}$ - b)

So, $\angle{}$OCB=$\angle{}$ OCE=45$^\circ{}$-b

Again, $\angle{}$ OBC=180$^\circ{}$-$\angle{}$ BOC -$\angle{}$ OCB = 180$^\circ{}$-135$^

\circ{}$-45$^\circ{}$+b = b

Again, $\angle{}$ DBO=180$^\circ{}$-$\angle{}$ BOD-b = 180$^\circ{}$-135$^\circ{}$-b =

45$^\circ{}$-b

Now, $\Delta{}$ DCB is a right ANGLE triangle

So, $BC^2+CD^2=BD^2$

Or, $BC^2+BC^2=BD^2$

Or, $2BC^2=BD^2$

So, $\frac{BC}{BD}=\frac{1}{\sqrt{2}}$

Now, in $\Delta{}$ DBO and $\Delta{}$ BOC --
\[
\angle{}\ DBO\ =\ \angle{}\ OCB\ =\ 45^\circ{}-b
\]
\[
\angle{}\ OBC\ =\ \angle{}\ BDO\ =\ b
\]
\[
\angle{}\ BOD\ =\ \angle{}\ BOC\ =\ 135^\circ{}\
\]
So, $\Delta{}$ DBO $\sim{}$ $\Delta{}$ BOC


So, $\frac{BD}{BC}=\frac{BO}{CO}$

Or, $\sqrt{2}=\frac{BO}{CO}$

Or, $\surd{}2CO=\ BO$

So, BO = $\surd{}$2CO [ ]