একের ভিতর তিন

তিনটি গাণিতিক সমস্যা ও সমাধান।

সমস্যা ১ :

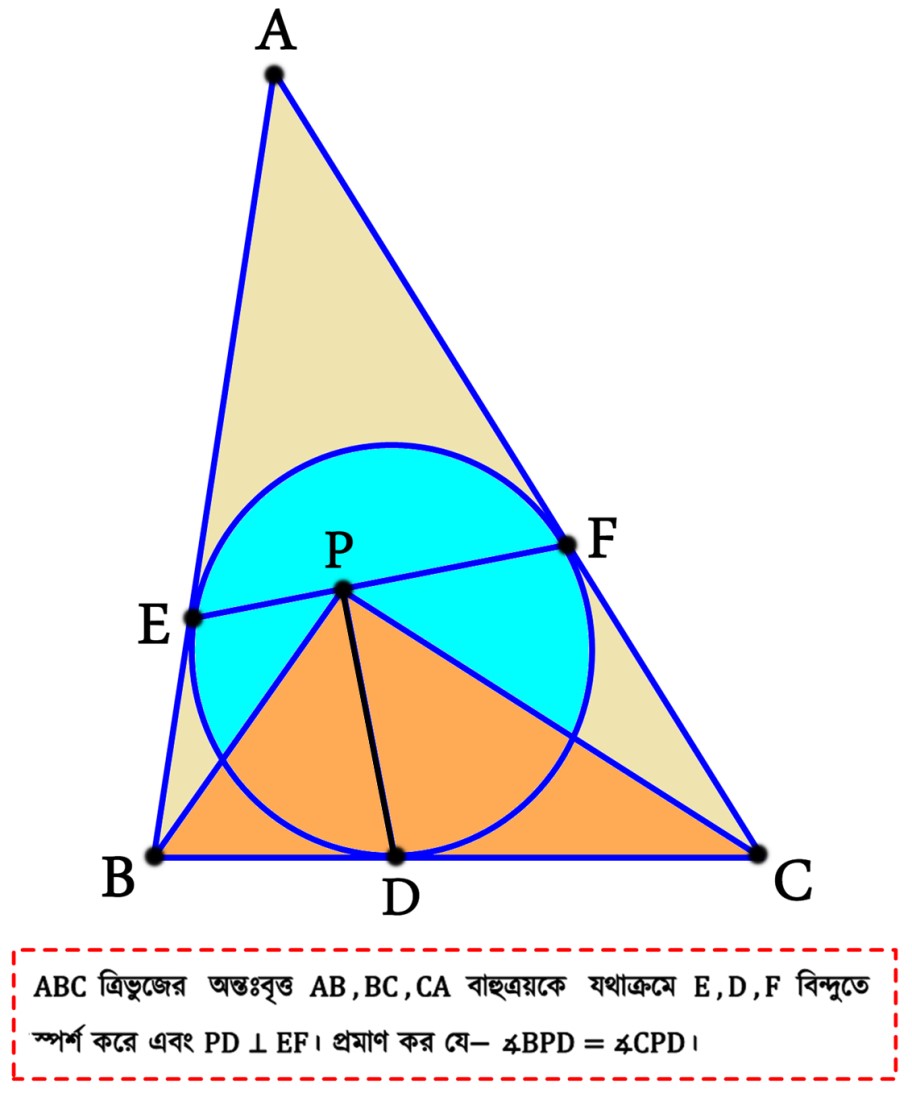
সমাধান ১:
আমরা জানি, বৃত্তের বহিঃস্থ কোন বিন্দু থেকে বৃত্তে দুইটি স্পর্শক টানলে, ঐ বিন্দু থেকে স্পর্শ বিন্দুদ্বয়ের দূরত্ব সমান।
এখন চিত্র থেকে দেখা যাচ্ছে- AE=AF , তাহলে ∠AEF=AFE
∴∠BEP=∠CFP
ধরি, অন্তর্বৃত্তের কেন্দ্র I। এইবার I ,B ;I ,D ;I ,F ;I ,E ;D ,E ও D ,F যোগ করি। তাহলে নতুন চিত্রটা হবে-

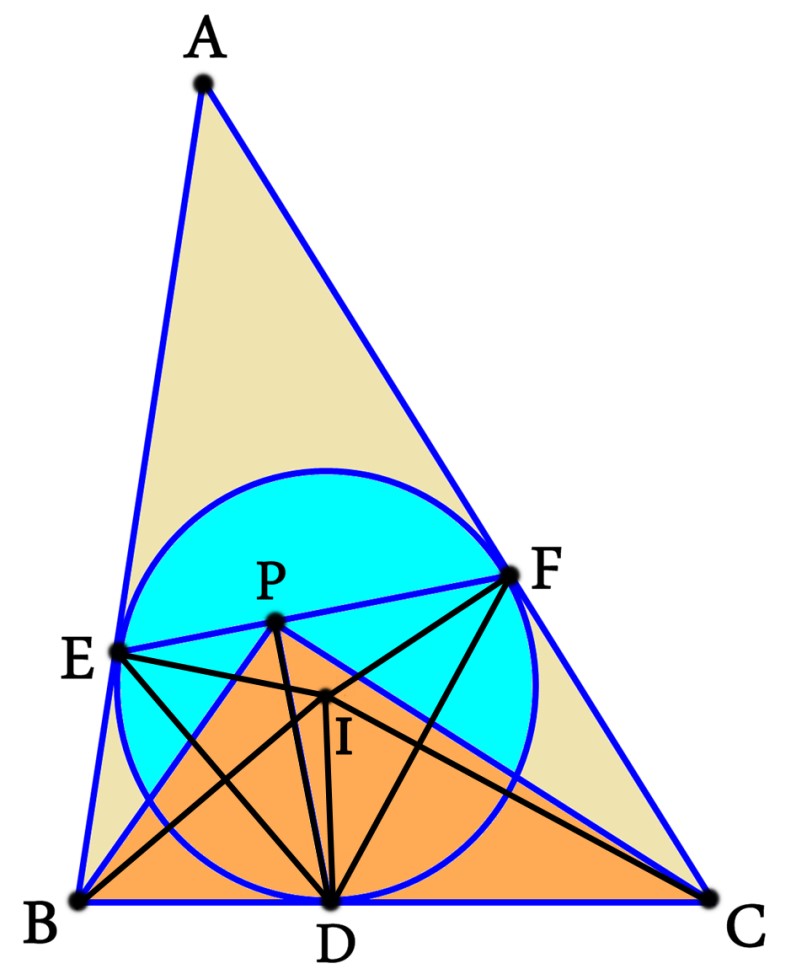
এখন, ∠BID=(∠DIE)/2=∠PFD
এখানে ∠BID=(∠DIE)/2 , কারণ BI ,∠DIE কে সমদ্বিখণ্ডিত করে এবং (∠DIE)/2=∠PFD , কারণ একই চাপের উপর দণ্ডায়মান বৃত্তস্থ কোণ (∠PFD) , কেন্দ্রস্থ কোণ (∠DIE) এর অর্ধেক।
∠IDB=∠DPF [উভয়ই এক সমকোণ]
এবং অবশিষ্ট ∠IBD= অবশিষ্ট ∠PDF
∴∆IBD ও ∆PDF সদৃশ ও সদৃশকোণী।
∴ID/PF=BD/PD … … … (i)
একইভাবে প্রমাণ করা যায় যে, ∆PDE ও ∆ICD সদৃশ ও সদৃশকোণী।
∴PE/ID=PD/CD … … … (ii)
(i)নং ও (ii)নং গুণ করে পাই, PE/PF=BD/CD
→PE/PF=BE/CF [∵CD=CF ,BD=BE]
এখন, ∆PEB ও ∆PFC হতে পাই, ∠PEB=∠PFC এবং PE/PF=BE/CF
আবার আমরা জানি, দুইটি ত্রিভুজের একটির এক কোণ অপরটির এক কোণের সমান হলে এবং সমান সমান কোণ সংলগ্ন বাহুগুলো সমানুপাতিক হলে, ত্রিভুজদ্বয় সদৃশ হবে।
∴∆PEB ও ∆PFC সদৃশ ও সদৃশকোণী।
∴∠BPE=∠CPF … … … (iii)
এখন, ∠DPE=∠DPF
→∠EPB+∠BPD=∠CPD+∠CPF
→∠BPE+∠BPD=∠CPD+∠BPE [(iii)নং হতে]
∴∠BPD=∠CPD
তাহলে আমাদের ১ম সমস্যার প্রমাণ হয়ে গেল। আশাকরি বুঝতে কোনো সমস্যা হয়নি। আমরা আমাদের ২য় সমস্যায় চলে যাই।

সমস্যা ২ :

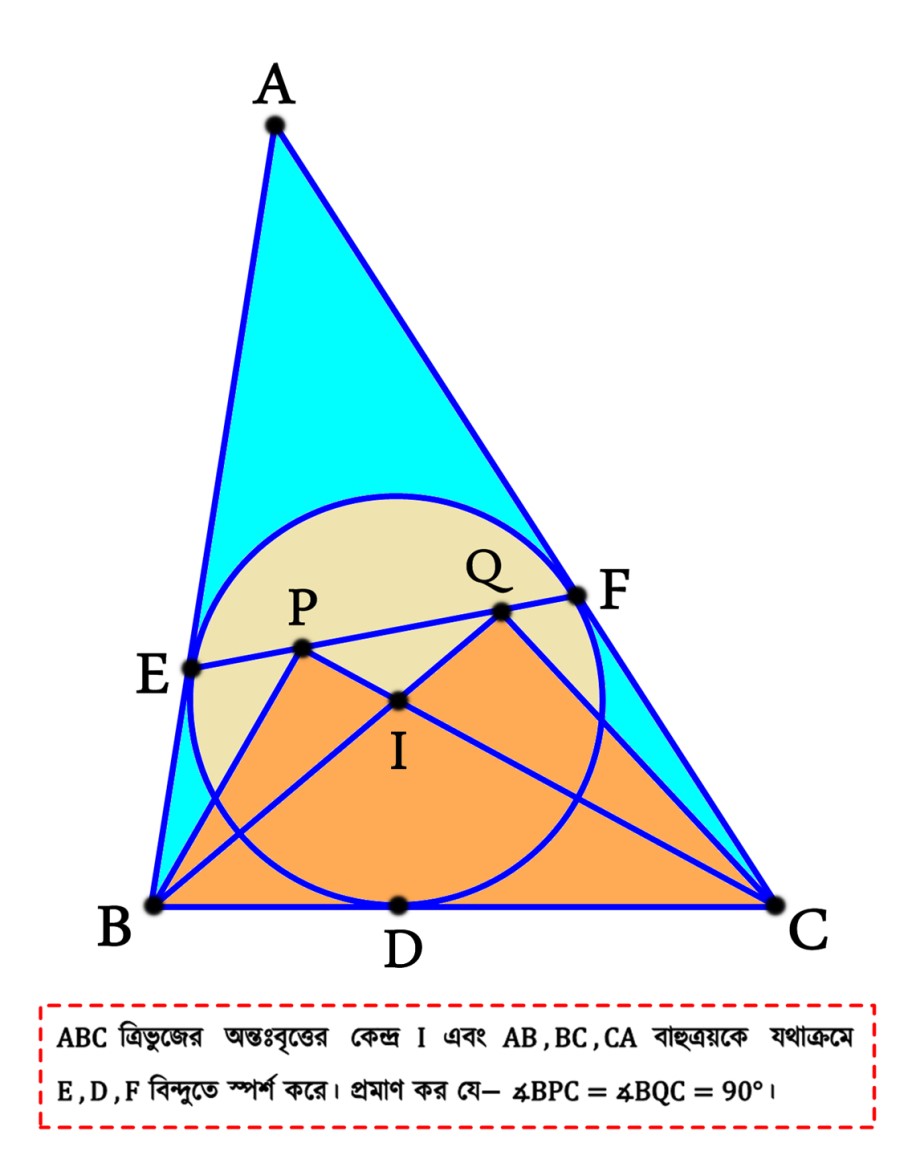
সমাধান ২:
সমস্যা-১ এ আমরা প্রমাণ করেছিলাম ∆PEB ও ∆PFC সদৃশ ও সদৃশকোণী।
তাহলে, ∠PBE=∠PCF
এখন, A বিন্দু থেকে EF এর লম্ব আঁকি যা I বিন্দু দিয়ে যাবে। আচ্ছা কেনো EF লম্ব I দিয়ে যাবে ?
দেখো ∆AEF একটি সমদ্বিবাহু ত্রিভুজ যার AE=AF। আবার ∆EIF একটি সমদ্বিবাহু ত্রিভুজ যার IE=IF। এখন যদি A বিন্দু থেকে EF এর অঙ্কিত লম্ব EF কে যে বিন্দুতে সমদ্বিখন্ডিত করবে, I বিন্দু থেকেও EF এর অঙ্কিত লম্ব EF কে সে একই বিন্দুতেই সমদ্বিখন্ডিত করবে। তাই A বিন্দু থেকে EF এর অঙ্কিত লম্ব I বিন্দুগামী। তাহলে চিত্রটা হবে-

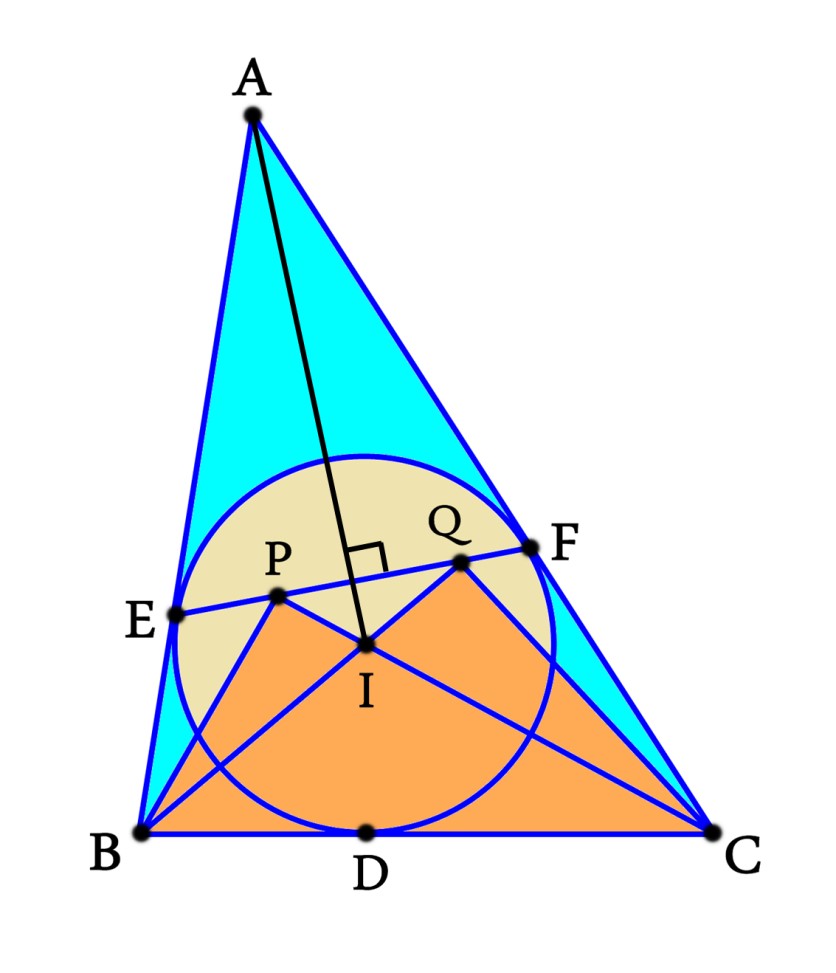
এখন, ∠EAI=∠FAI=(∠A)/2 , কারণ ত্রিভুজের শীর্ষবিন্দু ও ঐ ত্রিভুজের অন্তর্বৃত্তের কেন্দ্রের সংযোজন রেখা শীর্ষবিন্দুস্থ কোণকে সমদ্বিখণ্ডিত করে। অর্থাৎ AI ,∠EAF এর সমদ্বিখণ্ডক।
তাহলে, ∠FEB=90°+(∠A)/2 [█(ত্রিভুজের একটি বাহু বর্ধিত করলে যে বহিঃস্থ কোণ উৎপন্ন হয় @তা বিপরীত অন্তঃস্থ কোণদ্বয়ের সমষ্টির সমান।)]
∴∠EQB=180°-(90°+(∠A)/2)-(∠B)/2=90°-((∠A + ∠B))/2=90°-90°+(∠C)/2=(∠C)/2
এখন চিত্রে লক্ষ্য দেখবে- BPQC চতুর্ভুজটি বৃত্তস্থ কেননা ∠EQB=∠BCP=(∠C)/2 এবং প্রত্যেক কোণ একই চাপ BP এর ওপর দণ্ডায়মান।
তাহলে, ∠BPC=BQC
আবার আমরা চিত্রের দিকে একটু লক্ষ্য করি- ∠EQB=(∠C)/2 এবং ∠ICF=(∠C)/2
তাহলে, ∠IQF+∠ICF=∠IQF+∠EQB=180° , ফলে IQFC চতুর্ভুজটি বৃত্তস্থ। কেননা আমরা জানি, কোনো চতুর্ভুজের দুইটি বিপরীত কোণ সম্পূরক হলে তার শীর্ষবিন্দু চারটি সমবৃত্ত হবে।
আবার আমরা জানি, বৃত্তের কোনো বিন্দুতে স্পর্শক ও ঐ স্পর্শবিন্দুগামী ব্যাসার্ধ পরস্পর লম্বভাবে অবস্থিত। অর্থাৎ IF⊥AC হবে।
এখন, ∠IQC=∠IFC=90° [উভয়ই একই চাপ IC এর ওপর দণ্ডায়মান ]
সুতরাং, ∠BPC=BQC=90°
সমস্যা-২ ও আমাদের প্রমাণ হয়ে গেল। এখন আমরা সমস্যা-৩ এ চলে যাবো। এই প্রবলেমটি এইবার Online Math Contest এ এসেছিলো।

সমস্যা ৩ :

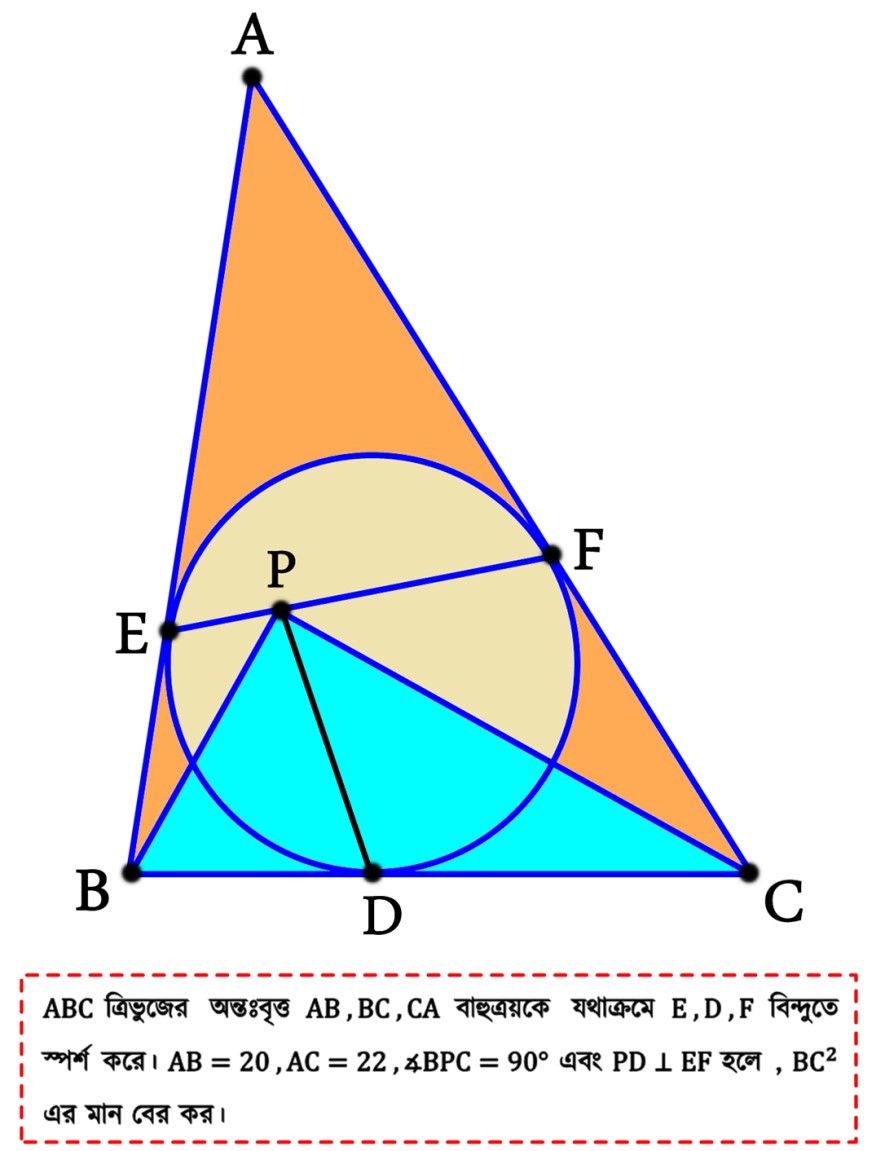
সমাধান ৩:
এই সমস্যা সমাধানে ক্ষেত্রে আমরা উপরের দুইটা সমস্যার সাহায্য নিবো। তার আগে আমরা প্রমাণের স্বার্থে কিছু অঙ্কন করব।
বিন্দু B থেকে অন্তর্বৃত্তের কেন্দ্রগামী একটি রেখা টানি যা EF কে Q বিন্দুতে ছেদ করে। C ,Q যোগ করি। চিত্রটা তাহলে হবে-

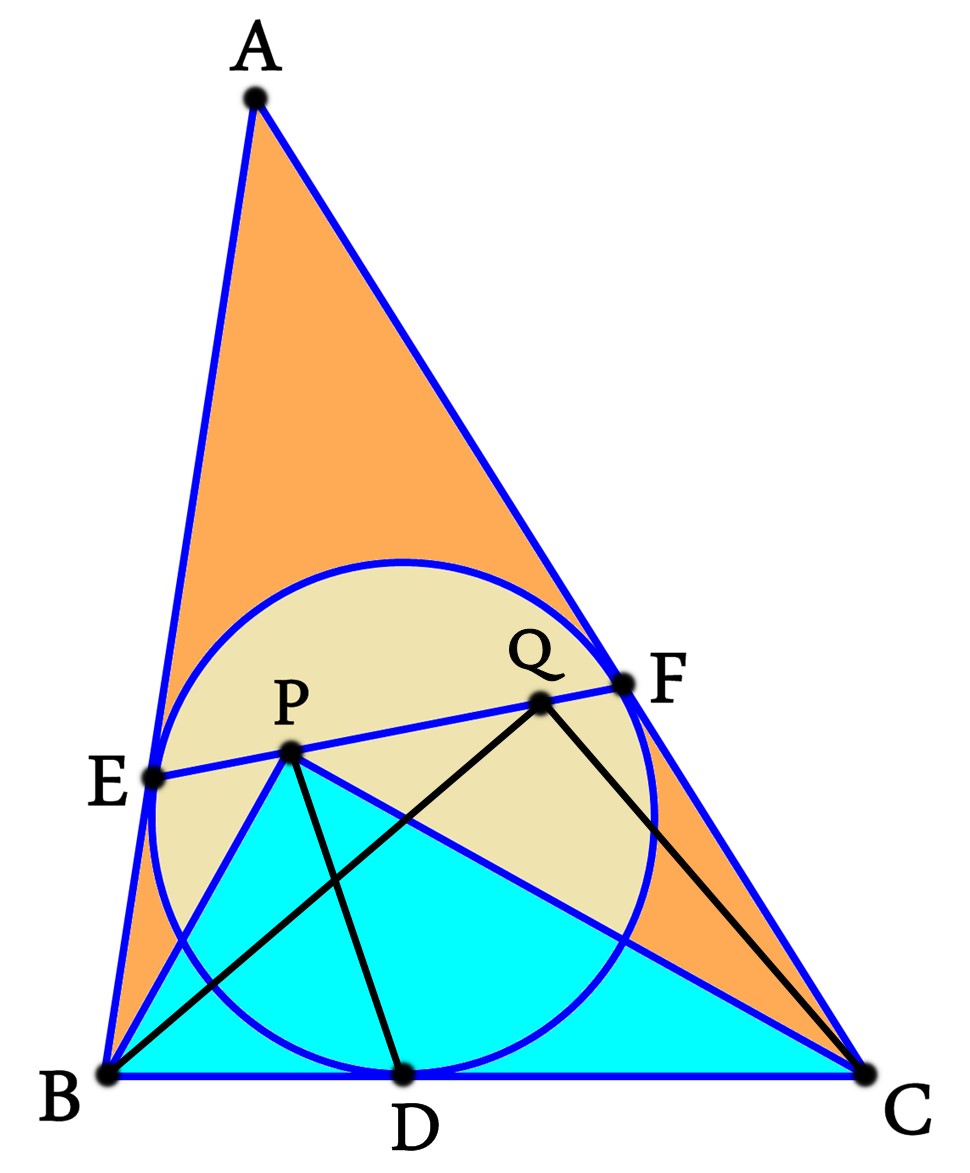
এখন, ∠BQC=90° হবে কারণ সমস্যা-২ তে আমরা প্রমাণ করেছি। চিত্র থেকে দেখা যাচ্ছে- BPQC চতুর্ভুজটি বৃত্তস্থ। কারণ ∠BPC=∠BQC=90°।
আবার প্রমাণ সমস্যা-২ তে দেখিয়ে ছিলাম ∠EQB=(∠C)/2। তাহলে, ∠BCP=(∠C)/2 হবে। কারণ একই চাপ BP এর দণ্ডায়মান বৃত্তস্থ কোণ। সুতরাং, CP রেখাটি অন্তর্বৃত্তের কেন্দ্র দিয়ে যাবে।
এখন, BPC সমকোণী ত্রিভুজ হতে পাই- ∠PBC+∠PCB=90°
→∠PBC+∠PCF=90°
→∠PBC+∠PBE=90° [∠PBE=∠PCF সমস্যা-১ প্রমাণ করা হয়েছে]
∴∠B=90°
সুতরাং, ABC একটি সমকোণী ত্রিভুজ যার ∠B=90°।
এখন, ABC একটি সমকোণী ত্রিভুজে পিথাগোরাস উপপাদ্য প্রয়োগ করে পাই-
AC^2=AB^2+BC^2
→BC^2=AC^2-AB^2
→BC^2=22^2-20^2
∴BC^2=84
যাক অবশেষে আমাদের সমস্যা-৩ ও সমাধান হয়ে গেল। আশা করি তোমাদের সবার জ্যামিতি তিনটি ভালো লাগবে।