Page 1 of 1
BdMO National 2021 Higher Secondary Problem 2
Posted: Sun Apr 11, 2021 9:03 pm
by Anindya Biswas
\(u\) আর \(v\) হলো দুটো বাস্তব সংখ্যা। নিচের রাশিটার সর্বনিম্ন মানকে যদি \(n\sqrt{n}\) আকারে লেখা যায়, তাহলে \(10n\)-এর মান বের করো। \[\sqrt{u^2+v^2}+\sqrt{(u-1)^2+v^2}+\sqrt{u^2+(v-1)^2}+\sqrt{(u-1)^2+(v-1)^2}\]
Let $u$ and $v$ be real numbers. The minimum value of \[\sqrt{u^2+v^2}+\sqrt{(u-1)^2+v^2}+\sqrt{u^2+(v-1)^2}+\sqrt{(u-1)^2+(v-1)^2}\] can be written as $n\sqrt{n}$. Find the value of $10n$.
Re: BdMO National 2021 Higher Secondary Problem 2
Posted: Sun Apr 11, 2021 10:12 pm
by Pro_GRMR
Anindya Biswas wrote: ↑Sun Apr 11, 2021 9:03 pm
Let $u$ and $v$ be real numbers. The minimum value of \[\sqrt{u^2+v^2}+\sqrt{(u-1)^2+v^2}+\sqrt{u^2+(v-1)^2}+\sqrt{(u-1)^2+(v-1)^2}\] can be written as $n\sqrt{n}$. Find the value of $10n$.
Can we use any Idea of symmetry here?
Solution :
Posted: Mon Apr 12, 2021 3:08 pm
by Anindya Biswas
$\text{Lemma :}$ \[\sqrt{a_1^2+b_1^2}+\sqrt{a_2^2+b_2^2}\geq\sqrt{\left(a_1+a_2\right)^2+\left(b_1+b_2\right)^2}\] For all real numbers $a_1,b_1,a_2,b_2$.
$\text{Proof :}$
Let's assume $a_1,b_1,a_2,b_2\in\mathbb{R}$
\[
\begin{equation}
\begin{split}
& (a_1b_1+a_2b_2)^2+(a_1b_2-a_2b_1)^2 \geq (a_1b_1+a_2b_2)^2 \\
& \Longrightarrow \left(a_1^2+b_1^2\right)\left(a_2^2+b_2^2\right)\geq (a_1b_1+a_2b_2)^2 \\
& \Longrightarrow \sqrt{(a_1^2+b_1^2)(a_2^2+b_2^2)}\geq \lvert a_1b_1+a_2b_2\rvert \geq a_1b_1+a_2b_2 \\
& \Longrightarrow a_1^2+b_1^2+a_2^2+b_2^2+2\sqrt{(a_1^2+b_1^2)(a_2^2+b_2^2)} \geq a_1^2+2a_1b_1+b_1^2+a_2^2+2a_2b_2+b_2^2 \\
& \Longrightarrow \left(\sqrt{a_1^2+b_1^2}+\sqrt{a_2^2+b_2^2}\right)^2 \geq \left(a_1+a_2\right)^2+\left(b_1+b_2\right)^2 \\
& \Longrightarrow \sqrt{a_1^2+b_1^2}+\sqrt{a_2^2+b_2^2} \geq \sqrt{\left(a_1+a_2\right)^2+\left(b_1+b_2\right)^2} \\ &\text{Q.E.D.}
\end{split}
\end{equation}
\]
According to this lemma,
\[
\begin{equation}
\begin{split}
& \sqrt{u^2+v^2}+\sqrt{(u-1)^2+v^2}+\sqrt{u^2+(v-1)^2}+\sqrt{(u-1)^2+(v-1)^2} \\
& \geq \sqrt{\left(u+\left(1-u\right)+u+\left(1-u\right)\right)^2+\left(v+\left(1-v\right)+v+\left(1-v\right)\right)^2} \\
& = \sqrt{2^2+2^2} \\
& = 2\sqrt{2}
\end{split}
\end{equation}
\]
And this minimum can be achieved when $u=v=\dfrac12$.
So, according to the question, $n=2$,
Therefore, our answer is $\boxed{10n=20}$
Geometric Interpretation :
Posted: Mon Apr 12, 2021 3:42 pm
by Anindya Biswas
Let's assume we start at $(0,0)$
Then we go to $(u,v)$ along a straight line.
Then we go to $(1,1)$ from there along a straight line.
From there, we go to $(1+u,2-v)$.
Then finally, we reach $(2,2)$ from there.
The total length of the path that we took to reach $(2,2)$ from $(0,0)$ is,
\[\sqrt{u^2+v^2}+\sqrt{(1-u)^2+(1-v)^2}+\sqrt{u^2+(1-v)^2}+\sqrt{(1-u)^2+v^2}\]
The minimum distance from the origin $(0,0)$ to $(2,2)$ is,
\[\sqrt{(2-0)^2+(2-0)^2}=2\sqrt{2}\]
Hence, $2\sqrt{2}$ is the minimum value of the above expression.
Here's the visualization :
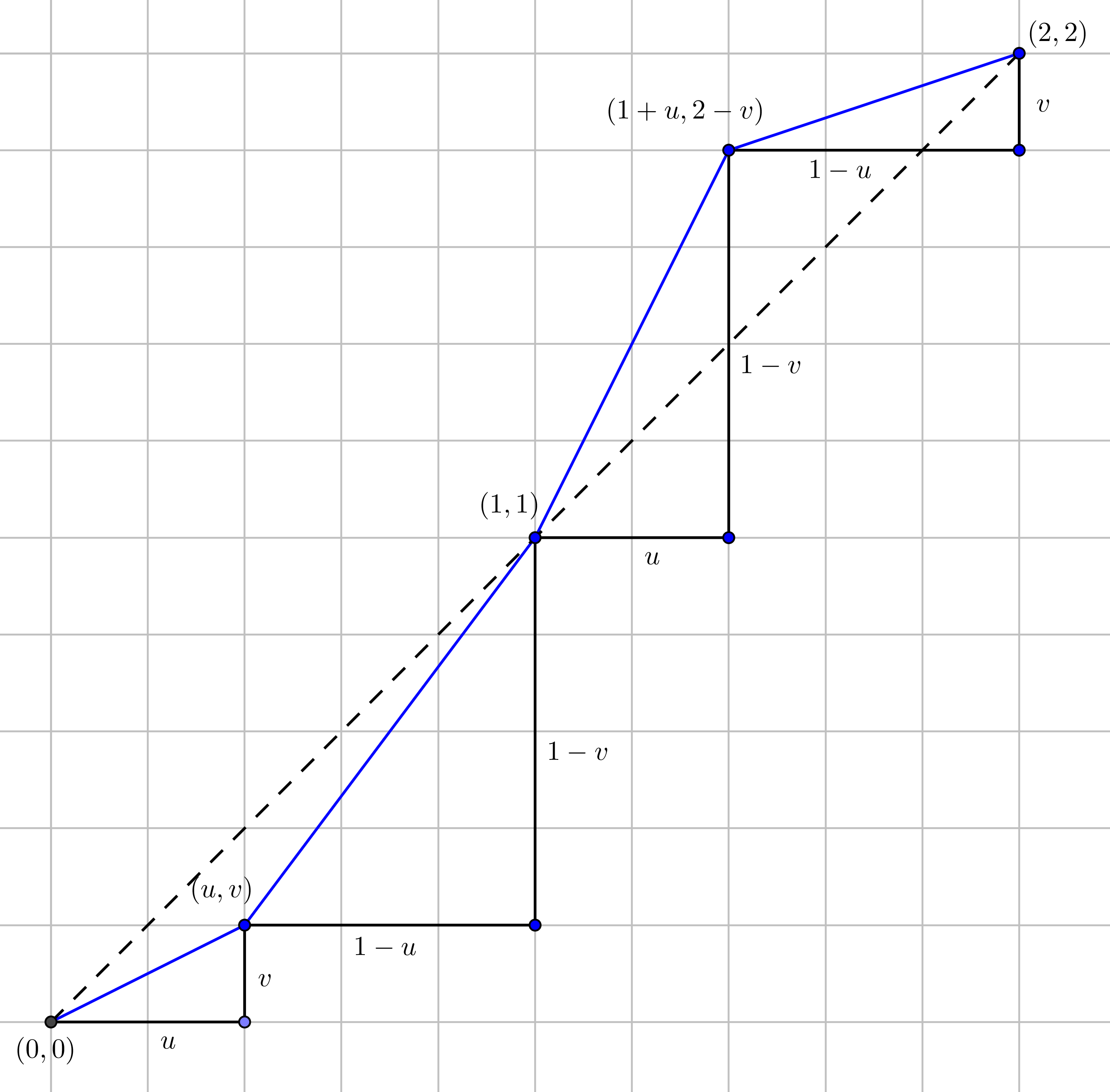
- The blue path we took vs. the minimum path we could take
- BdMO 2021 HS 2.png (142.6KiB)Viewed 3533 times