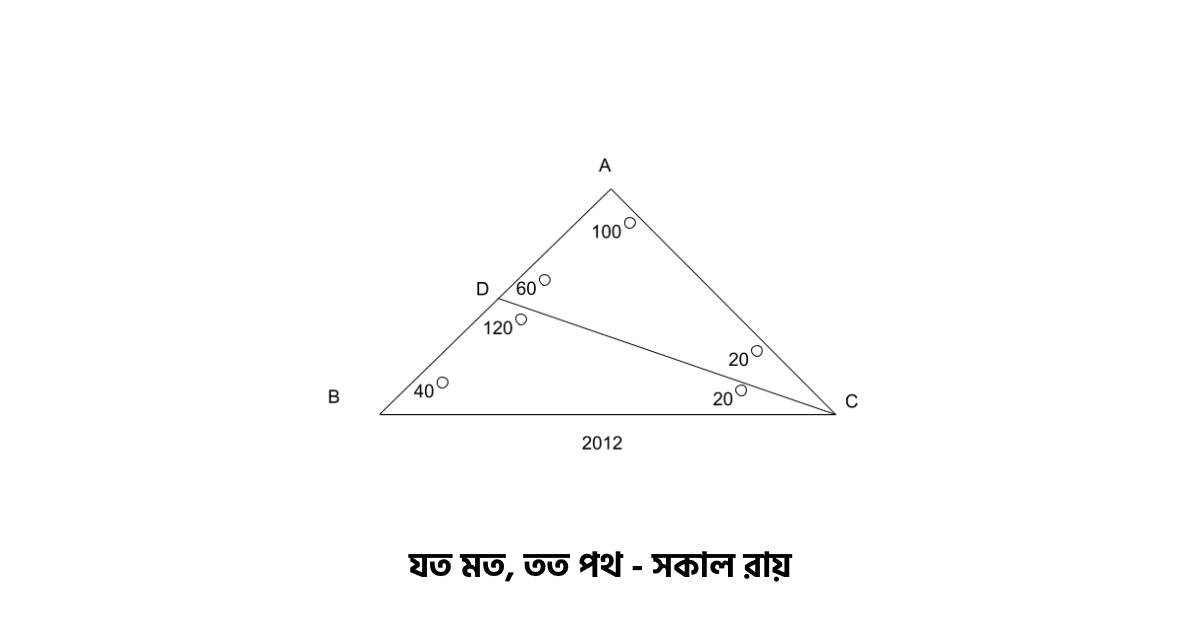
ΔABC এ ∠A = 100°, AB = AC । AB এর উপর D একটি বিন্দু যেন CD , ∠ACB কে সমদ্বিখণ্ডিত করে। BC= 2012 হলে (AD+CD) = ?
সমাধানঃ
বোকাসোকা মানুষের অস্ত্রঃ ত্রিকোণমিতি
ত্রিকোণমিতির জন্য আমাদের দরকার অনেক অনেক কোণের মান।
শুরুতেই দেখি প্রশ্ন থেকে কতগুলো কোণের মান আমরা সরাসরি জানি অথবা কোনভাবে মান বের করতে পারি। চলো দেখা যাক,
∠A = 100°, AB = AC তাহলে, ∠ABC = ∠ACB = (180°-100°)/2 = 80°/2 = 40°
আবার, CD , ∠ACB কে সমদ্বিখণ্ডিত করে। অর্থাৎ, ∠ACD = ∠BCD= 40°/2 = 20°
এখন, ∠ADC = 180° - ∠DAC - ∠ACD = 180° - 100° - 20° = 60°
বাকি থাকে একটা কোণ, ∠BDC।
এবার, ∠BDC = 180° - ∠ADC = 180° - 60° = 120°
সব মিলিয়ে চিত্রটা দেখতে হবে নিচের মত।
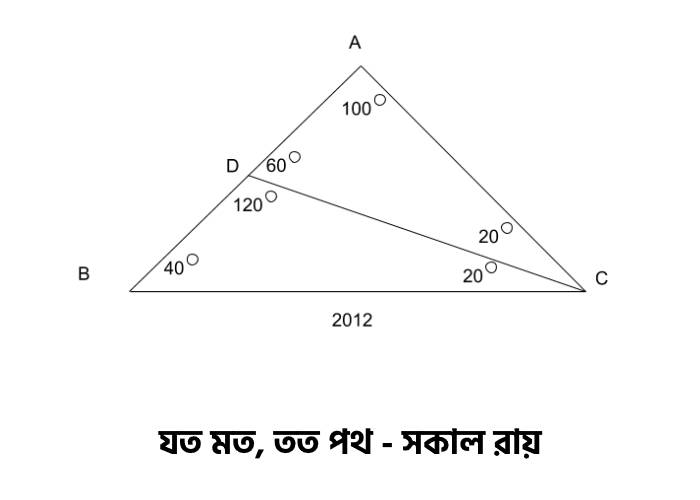
এবার, ত্রিকোণমিতির খেলা শুরু। বেশি বেশি কোণ থাকলে আমার যে বন্ধুর কথা মনে পড়ে সে হচ্ছে সাইন সূত্র। চলো দেখা যাক আমার বন্ধু সাইন সূত্র কি বলে?
এখানে, দেখা যাচ্ছে মাত্র একটা বাহুর দৈর্ঘ্য আমরা জানি আর সেটা হচ্ছে BC =2012. কাজেই আমাদের উদ্দেশ্য হচ্ছে AD এবং CD কে BC এর মাধ্যমে প্রকাশ করা।
ΔBDC থেকে পাই,
CD / sin 40° = BC / sin 120°
বা, CD = ( BC sin 40° ) / sin 120°
বা, CD = ( 2012 sin 40° ) / (√3 /2)
বা, CD = (4024 sin 40°) /√3
ΔADC থেকে পাই,
AD / sin 20° = CD / sin 100°
বা, AD = CD (sin 20° / sin 100°)
বা, AD = (4024 sin 40°) /√3 x (sin 20° / sin 100°) [যেহেতু, CD = (4024 sin 40°) /√3 ]
বা, AD = 4024 sin 40°sin 20° / (√3 sin 100°)
বা, AD = 4024 sin 40°sin 20° / [√3 sin (90°+10°)]
বা, AD = 4024 sin 40°(2 sin 10° cos 10°) / (√3 cos 10°)
বা, AD = 8048 sin 40° sin 10° / √3
এখন, AD+CD
= 8048 sin 40° sin 10° / √3 + (4024 sin 40°) /√3
= 4024 /√3 ( 2 sin 40° sin 10° + sin 40°)
= 4024 /√3 [cos (40°- 10°) - cos (40° + 10°) + sin (90° - 50°)]
= 4024 /√3 [cos 30° - cos 50° +cos 50°]
= 4024 /√3 x (√3 /2)
= 2012
অর্থাৎ, AD + CD = 2012.
জ্যামিতির পথে পথচলা
একটু আধটু কষ্ট করতে রাজী থাকলে আরো একভাবে করা যায় এই সমস্যার সমাধান।
জ্যামিতির কিছু মজার মজার উপপাদ্য আছে সেগুলো ব্যবহার করে এবং আরো কিছু আঁকাআঁকি করে এই সমস্যাটি সমাধান করা যায়। এখন যেভাবে প্রমাণ করা হবে সেটা গণিত অলিম্পিয়াড প্রস্তুতির লক্ষ্যে প্রকাশিত বিভিন্ন বইতে তোমরা হয়তো দেখেছো। যেমন- গণিতের স্বপ্নযাত্রা বইতে একটু খুঁজলেই পেয়ে যাবে।
“কোন ত্রিভুজের একটি কোণের অন্তর্দ্বিখন্ডক ঐ কোণের বিপরীত বাহুদুটিকে কোণের সংলগ্ন বাহুদ্বয়ের অনুপাতে অন্তর্বিভক্ত করে।” - এই উপপাদ্য ব্যবহার করে এটি করা যায়।
[ গণিতের স্বপ্নযাত্রা বই থেকে প্রমাণটা দেখে নিও ]
বিরাট ফাঁকিবাজি
এইবার আমরা ঘুরে আসবো ফাঁকিবাজির দুনিয়ায় । আমরা এবার ত্রিকোণমিতি ব্যবহার করবো না। আবার নতুন কোন উপপাদ্যও ব্যবহার করবো না। শুধু একটু আঁকাআঁকি করেই সমাধান হয়ে যাবে এই সমস্যার। বিশ্বাস না হলে নিজেই দেখে নাও।
আমরা তিনটা নতুন রেখা আঁকবো।
১) BC এর সমান্তরাল করে DE রেখা আঁকবো।
২) B,E যোগ করবো।
৩) BC থেকে CD এর সমান করে CF কেটে নিয়ে D,F যোগ করবো।
এখন, যে ধারণাটা ব্যবহার করে আমরা একটা বিশাল ফাঁকি দিবো সেটা হল প্রতিসমতা (Symmetry)।
যেহেতু, ΔABC এ AB = AC তাই ছবি অনুসারে ডান এবং বাম দুদিকে থেকেই দেখতে একই রকম।
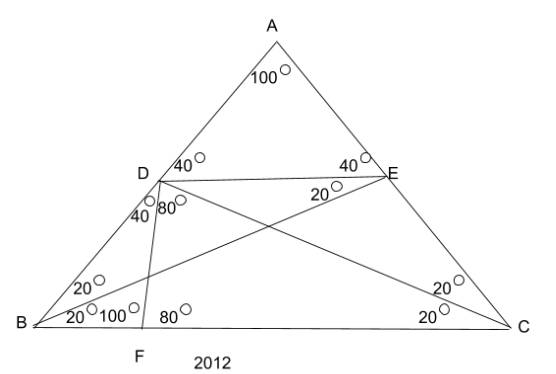
এখন, DE এবং BC সমান্তরাল হলে, BE , ∠ABC কে সমদ্বিখণ্ডিত করবে।
অর্থাৎ, ∠ABE = ∠CBE= 40°/2 = 20°
আবার, DE এবং BC সমান্তরাল তাই , ∠ADE = ∠AED= 40° এবং, ∠DEB = 20°
তাহলে, ∠DEB = ∠DBE = 20° তাই, DB = DE
এখন, CD = CF এবং, ∠DCF = 20° , তাই, ∠CDF = ∠CFD= (180° - 20°)/2 = 80°
অর্থাৎ, ∠BFD = (180° - 80°) = 100° এবং, ∠BDF = (180° - 40° - 100°) = 40°
এখন, ΔADE ও ΔFDB এর মধ্যে DB = DE এবং, ∠ADE = ∠FDB = 40° ∠AED = ∠FBD = 40°
তাহলে, ΔADE ও ΔFDB সর্বসম।
অর্থাৎ, BF = AD
এবারে, AD + CD = BF + CF = BC =2012.
ব্যস, সমাধান হয়ে গেলো।
তাহলে দেখলে তো, নিত্যনতুন পথে সমাধান করায় কোন বাধা নেই। এমন আরো মজার মজার জ্যামিতির সমস্যার বিভিন্ন সমাধান নিয়ে দেখা হবে তোমাদের সাথে।